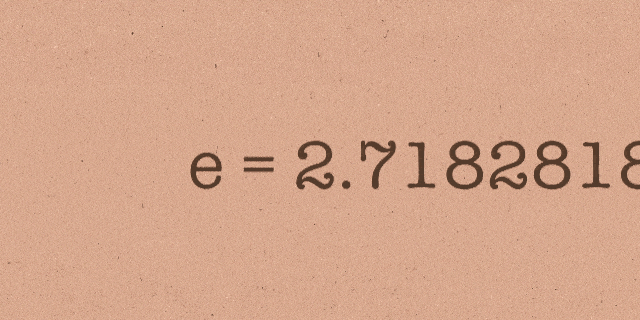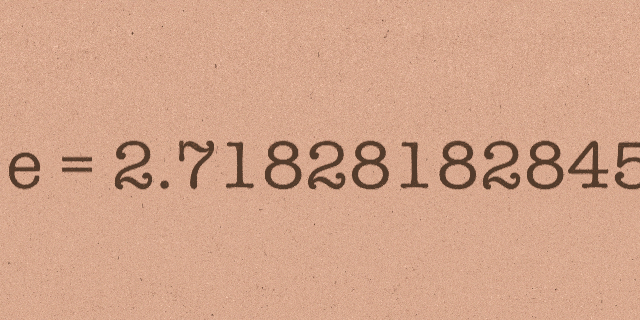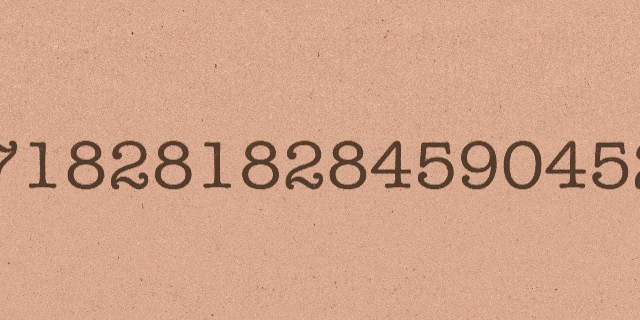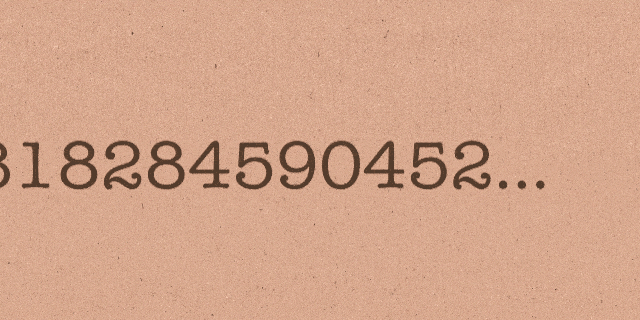
Matematikte sürekli karşımıza çıkan, işlemlerimizde sıklıkla kullandığımız en çok bilinen iki özel sayı vardır. Bunlardan biri π (pi) sayısıdır. π sayısını yine nispeten anlayabiliyoruz. Nasıl bulunur? Nerelerde kullanılır? Bunları kestirmek biraz daha kolay. π sayısının en kolay anlatımı, “bir çemberin çevresinin çapına bölümünden doğan sayı” ifadesidir. Fakat diğer özel sayımız olan e sayısının nasıl bulunduğunu ve nerede? niye? kullanıldığını tam olarak bilemeyebiliyoruz. Bu yazıda e sayısı ile aramızda olan mesafeyi biraz daha azaltacağız.
Bu sabit ise adını fazla kimsenin duymadığı e sayısıdır. Bazı matematikçilerin Euler sayısı olarak da adlandırdığı Euler sabiti irrasyonel bir sayıdır, yani onu bir kesir olarak ifade edemezsiniz. Bu sayı 2,718281… olarak başlar ve diğer aşkın sayılar gibi sonsuza kadar devam eder.
Not: Matematikte cebirsel olmayan herhangi bir reel sayıya aşkın sayı denir. Diğer bir deyişle, katsayıları tamsayı (ya da rasyonel) olan bir polinomun kökü olamayan reel sayılara aşkın sayı denir.
e sayısı nüfus artışını belirlemede, finansal matematikle uğraştığımız zamanlarda, olasılık ve istatistik hesaplamalarında, tüm üniversite öğrencilerinin aşina olduğu çan eğrisinin hesaplanmasında, bilimde birbirini tekrar eden deneylerin başarı olasılıklarının hesaplanmasında, hatta işe alım gibi süreçlerin belirlenmesinde bile kullanılmaktadır!
Bu sabitin nasıl oluştuğunu daha iyi anlamak için basit bir örneğe bakalım.
Yatırım konusunda bilgili arkadaşınızın 100 TL istediğini ve bunu bir yılda ikiye katlayabileceğini iddia ettiğini hayal edin. Yıl sonunda size 200 TL vererek %100 yatırım getirisini garanti eder. Eğer bu doğruysa, yatırımınızı 6 ay içinde geri isterseniz, teorik olarak size %50’lik bir getiri sağlamalıdır, bu da toplam 150 TL’dir. 6 ayın sonunda 150 TL alır ve kalan 6 ay için “fonuna” geri koyarsanız, yılın sonunda 225 TL alırsınız. Bu ekstra 25 TL demek.

Şimdi, her ay paranızı alıp yeniden yatırım yapsanız ne olur? Yaklaşık 271 TL kazanıyor olacaksınız. Peki ya her günün sonunda paranızı çekerseniz? Yaklaşık 271.82 TL kazanacaksınız… Bunun nereye gittiğini görüyor musunuz? Paranızı ikiye katlamak yerine katlanarak büyütmeyi başardınız. Başka bir deyişle, paranızı bir “e” faktörü kadar büyüttünüz.
Ve sonucunda elde ettiğimiz sayı, Euler Sayısı’nın bir yakınsamasıdır. Ne kadar minik parçaya bölerseniz bölün, bu sayı asla ve asla 2.72 TL’ye ulaşmayacaktır. Sınır, e sayısıdır.
► Yılda %100 faiz veren bir bankaya yatırırsa 1 sene sonra 2 lirası olur.
► 6 ayda bir %50 faiz veren bir bankaya yatırırsa 1 sene sonra 2,25 lirası olur.
► 3 ayda bir %25 faiz veren bir bankaya yatırırsa 1 sene sonra 2,44… lirası olur.
► Ayda bir %8,33… faiz veren bir bankaya yatırırsa 1 sene sonra 2,6130… lirası olur.
► Ve aynı şekilde haftada bir işleyen faiz sonunda 1 sene sonra 2,6925… lirası olur.
► Her gün işleyen faizi hesapladığımızda ise 1 sene sonra 2,71453… lirası olur.
